Kod: Zaznacz cały
Zabrałem się za opisanie zastosowania trójkątów Pitagorejskich w budowaniu z LEGO. Tekst się rozrastał w miarę pisania i osiągnął gigantyczną długość. Niewielką część przedstawionych zależności stosowałem w prowadzonych "warsztatach" na wystawach, o czym opowiadam we właściwym momencie. Żeby ułatwić odwoływanie się do tekstu w komentarzach, ponumerowałem cztery główne części oraz wszystkie zdjęcia i tabele. Przez sqrt(x) rozumiem pierwiastek (stopnia drugiego) z liczby x, np. sqrt(25)=5. Miłej lektury!1. Najbardziej znana trójka Pitagorejska.
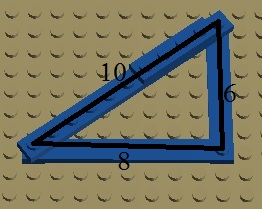
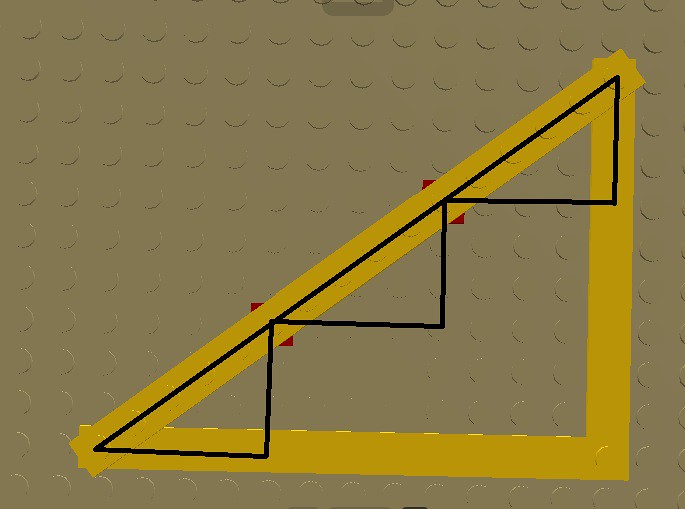
Każdy z nas po edukacji szkolnej jest w stanie wymienić trójkę Pitagorejską: 3, 4, 5, czyli trzy liczby naturalne będące bokami trójkąta prostokątnego, a więc spełniające zależność z twierdzenia Pitagorasa: a^2 + b^2 = c^2. W podanym przykładzie boki o długościach 3 i 4 są przyprostokątnymi, a bok o długości 5 jest przeciwprostokątną. Korzystając z podobieństwa trójkątów, na podstawie podanego przykładu można bez trudu podać nieskończenie wiele układów liczb naturalnych stanowiących długości boków kolejnych trójkątów prostokątnych: powiększając każdy z boków dwa razy, dostaje się trójkąt o bokach 6, 8, 10; po trzykrotnym powiększeniu mamy 9, 12, 15, itd.
Realizacja tych trójkątów klockami systemowymi wygląda następująco:

Rys. 1.1.

Rys. 1.2.
Rys. 1.3.
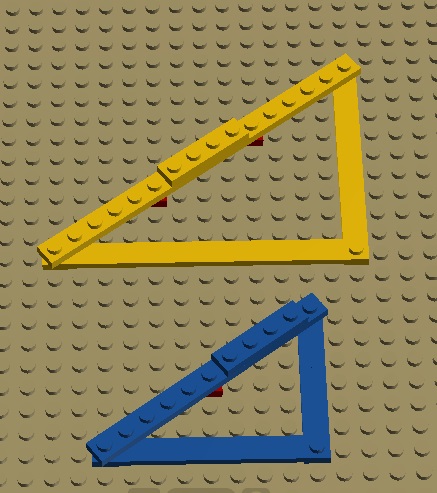
Rys. 1.4.

Rys. 1.5.
Rys. 1.6.

Rys. 1.7.

Rys. 1.8.

Rys. 1.9.
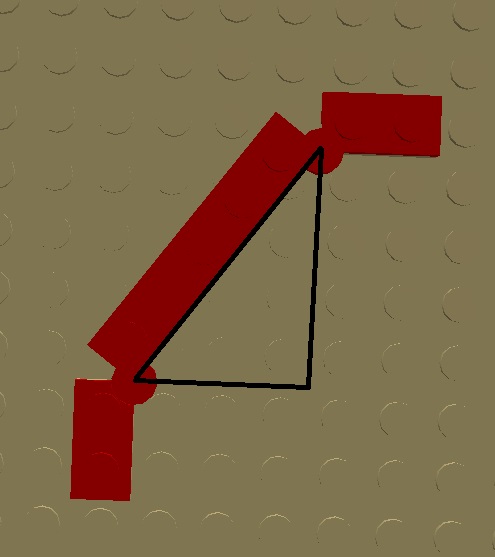
Istnieje jeszcze drugi sposób uzyskania omwianej serii trójkątów, mianowicie za pomocą zawiasów.

Rys. 1.10.
Rys. 1.11.



Rys. 1.12abc.
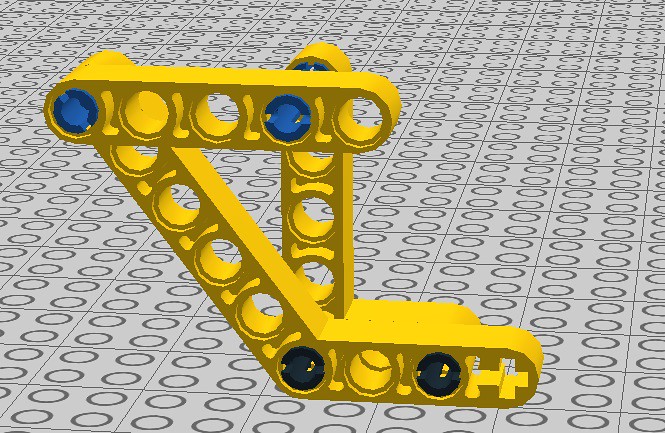
Rys. 1.13.
* przedniej szybie w 42075, Fire Responder:

Rys. 1.14.

Rys. 1.15.

Rys. 1.16.

Rys. 1.17.
* przedniej szyby w 42069, Extreme Adventure:

Rys. 1.18.

Rys. 1.19.

Rys. 1.20.
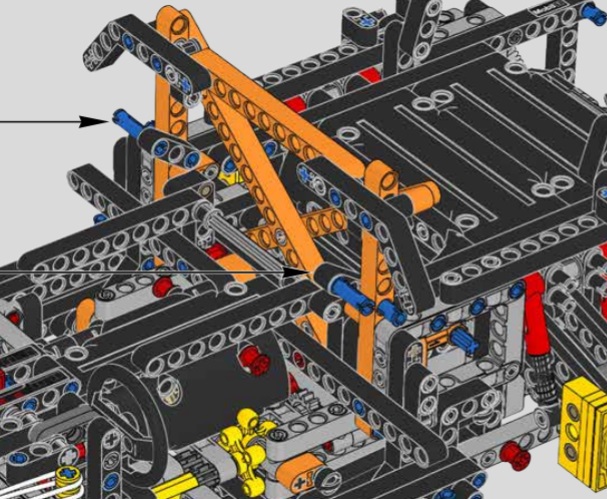
Rys. 1.21.
Wśród klocków serii Technic znajdziemy jeszcze dwie części zaprojektowane z myślą o omawianych trójkątach. Pierwszą z nich jest następujący panel:

Rys. 1.22.

Rys. 1.23.

Rys. 1.24.
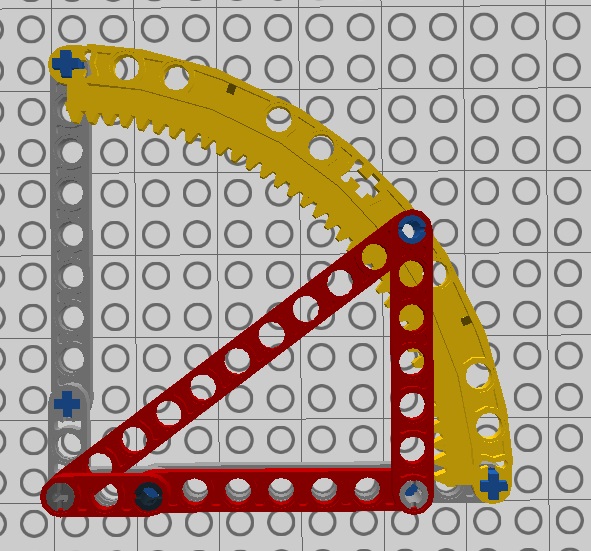
Rys. 1.25.
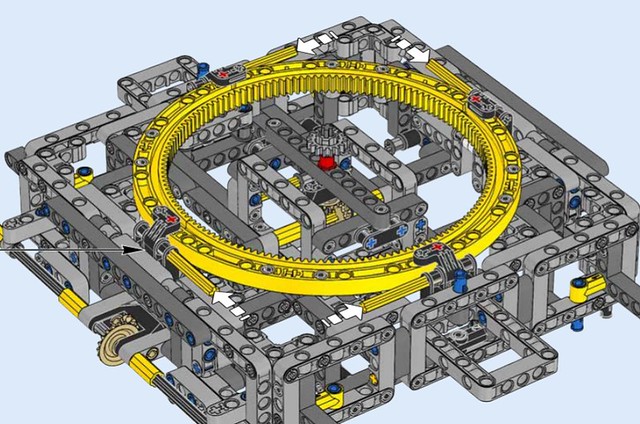
Rys. 1.26.
Układ liczb 3, 4, 5 nie jest jedyną pierwotną (czyli w dużym skrócie nieskracalną) trójką Pitagorejska. Kolejne takie układy to:
Kod: Zaznacz cały
(3, 4, 5) (5, 12, 13) (8, 15, 17) (7, 24, 25)
(20, 21, 29) (12, 35, 37) (9, 40, 41) (28, 45, 53)
(11, 60, 61) (16, 63, 65) (33, 56, 65) (48, 55, 73)
(13, 84, 85) (36, 77, 85) (39, 80, 89) (65, 72, 97)Kod: Zaznacz cały
a = m^2 - n^2 b = 2*m*n c = m^2 + n^2Budując z klocków LEGO, bierzemy pod uwagę wszystkie trójkąty Pitagorejskie powstające z pierwotnych trójek Pitagorejskich oraz trójkąty do nich podobne powiększone całkowitą lub połówkową liczbę razy. Oto kilka przykładów: na czerwono trójkąt o bokach o długościach 5, 12 i 13 studów; na niebiesko trójkąt o bokach o długościach 16, 30 i 34 studów; na żółto trójkąt o bokach o długościach 10, 10,5 i 14,5 studów (czyli połówka z 20, 21, 29):
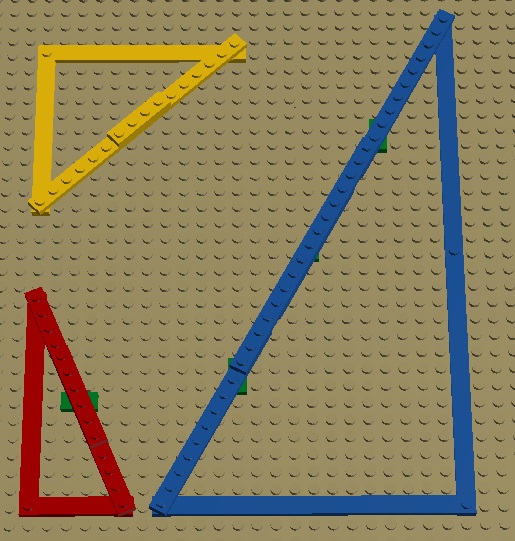
Rys. 2.1.

Rys. 2.2.

Rys. 2.3.
* w kolorowym łączeniu kokpitu ze statkiem w 75192, Millennium Falcon:
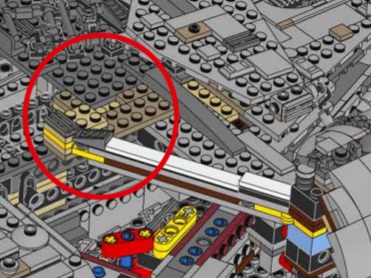
Rys. 2.4.

Rys. 2.5.
Kod: Zaznacz cały
trójka mniejszy większy
Pitagorejska kąt ostry kąt ostry
(15,112,113) 7,63 82,37
(13, 84, 85) 8,80 81,20
(11, 60, 61) 10,39 79,61
(20, 99, 101) 11,42 78,58
(9, 40, 41) 12,68 77,32
(16, 63, 65) 14,25 75,75
(7, 24, 25) 16,26 73,74
(12, 35, 37) 18,92 71,08
(5, 12, 13) 22,62 67,38
(36, 77, 85) 25,06 64,94
(39, 80, 89) 25,99 64,01
(8, 15, 17) 28,07 61,93
(33, 56, 65) 30,51 59,49
(28, 45, 53) 31,89 58,11
(60, 91, 109) 33,40 56,60
(3, 4, 5) 36,87 53,13
(48, 55, 73) 41,11 48,89
(65, 72, 97) 42,08 47,92
(20, 21, 29) 43,60 46,40
Kod: Zaznacz cały
Nazwa kolcka większy mniejszy tangensy
kąt ostry kąt ostry kątów
Wedge Plate 3x3 45,00 45,00 1; 1
Wedge Plate 2x2, left/right 63,43 26,57 2; 1/2
Wedge Plate 3x2, left/right 71,57 18,43 3; 1/3
Wedge Plate 4x2, left/right 75,96 14,04 4; 1/4
Wedge Plate 12x3, left/right 80,54 9,46 6; 1/6
Wedge Plate 4x9 84,29 5,71 10; 1/10
3. Inne trójkąty prostokątne.
Oczywiście trójkąt prostokątny nie musi mieć wszystkich boków o długościach całkowitych. Klocki LEGO mające rządek studów nie służą do budowania długości niewymiernych, są jednak przypadki, że i takie trójkąty powstają. Najczęściej mamy do czynienia z trójkątami, w których dwa boki mają długość całkowitą – i te boki jesteśmy w stanie zbudować, a jeden niewymierną – i ten bok nie jest fizycznie budowany. Patrząc inaczej na układ studów, można znaleźć szereg liczb niewymiernych:

Rys. 3.1.
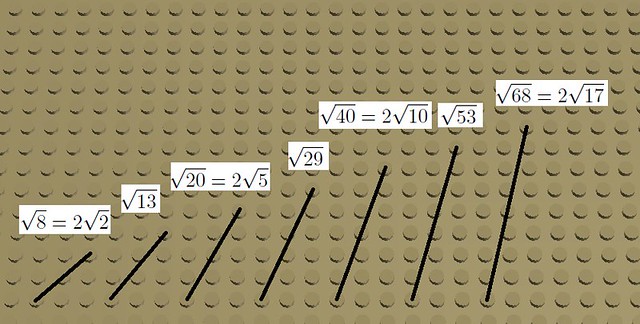
Rys. 3.2.

Rys. 3.3.
Rys. 3.4.

Rys. 3.5.
Kod: Zaznacz cały
trójkąt pierwszy trójkąt drugi (trójkąt trzeci)
1, 7, 5sqrt(2) 5, 5, 5sqrt(2)
1, 8, sqrt(65) 4, 7, sqrt(65)
2, 9, sqrt(85) 6, 7, sqrt(85)
2, 11, 5sqrt(5) 5, 10, 5sqrt(5)
3, 11, sqrt(130) 7, 9, sqrt(130)
1, 12, sqrt(145) 8, 9, sqrt(145)
1, 13, sqrt(170) 7, 11, sqrt(170)
4, 13, sqrt(185) 8, 11, sqrt(185)
3, 14, sqrt(205) 6, 13, sqrt(205)
5, 14, sqrt(221) 10, 11, sqrt(221)
9, 13, 5sqrt(10) 5, 15, 5sqrt(10)
3, 16, sqrt(265) 11, 12, sqrt(265)
1, 17, sqrt(290) 11, 13, sqrt(290)
4, 17, sqrt(305) 7, 16, sqrt(305)
1, 18, 5sqrt(13) 6, 17, 5sqrt(13) 10, 15, 5sqrt(13)
7, 17, 13sqrt(2) 13, 13, 13sqrt(2)
2, 19, sqrt(365) 13, 14, sqrt(365)
3, 19, sqrt(370) 9, 17, sqrt(370)
4, 19, sqrt(377) 11, 16, sqrt(377)
7, 19, sqrt(410) 11, 17, sqrt(410)
8, 19, 5sqrt(17) 13, 16, 5sqrt(17) 5, 20, 5sqrt(17)
1, 21, sqrt(442) 9, 19, sqrt(442)
2, 21, sqrt(445) 11, 18, sqrt(445)
9, 20, sqrt(481) 15, 16, sqrt(481)
1, 22, sqrt(485) 14, 17, sqrt(485)
3, 22, sqrt(493) 13, 18, sqrt(493)
8, 21, sqrt(505) 12, 19, sqrt(505)
1, 23, sqrt(530) 13, 19, sqrt(530)
2, 23, sqrt(533) 7, 22, sqrt(533)
4, 23, sqrt(545) 16, 17, sqrt(545)
6, 23, sqrt(565) 9, 22, sqrt(565)
7, 23, 17sqrt(2) 17, 17, 17sqrt(2)
9, 23, sqrt(610) 13, 21, sqrt(610)
2, 25, sqrt(629) 10, 23, sqrt(629)
11, 23, 5sqrt(26) 17,19, 5sqrt(26) 5, 25, 5sqrt(26) 
Rys. 3.6.

Rys. 3.7.

Rys. 3.8.

Rys. 3.9.
* na bazie deltoidu z dwoma kątami prostymi:

Rys. 3.10.

Rys. 3.11.
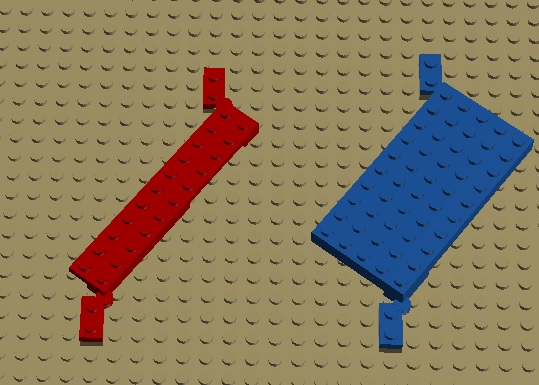
Rys. 3.12.

Rys. 3.13.
* deltoid z dwoma kątami prostymi:

Rys. 3.14.

Rys. 3.15.

Rys. 3.16.
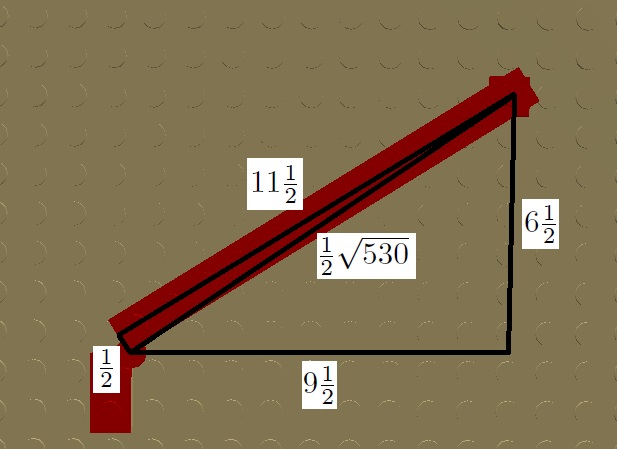
Rys. 3.17.
Wybranie linii z parzystymi liczbami całkowitymi wymusza użycie jumperów lub wpinanie w nietypowe miejsca na spodzie klocka, np. linia z pierwiastkiem 365 po podzieleniu przez 2 daje dwa trójkąty realizowane w następującej konstrukcji:

Rys. 3.18.
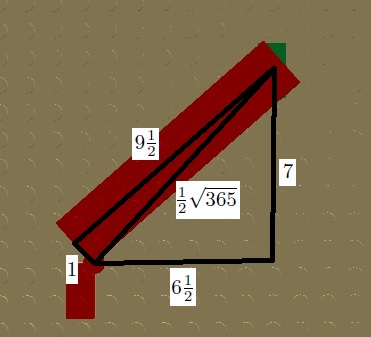
Rys. 3.19.

Rys. 3.20.
Dla osoby budującej interesujący jest kąt ułożenia ukośnego klocka. Można dowieść ścisłym rozumowaniem matematycznym, że zarówno w przykładach z deltoidami jak i w przykładach z trójkątami prostokątnymi o wspólnej przeciwprostokątnej ułożenie ukośnych klocków jest zawsze pod kątem, który możemy znaleźć w jednym z trójkątów Pitagorejskich.
Bezpośrednia z rachunków w dowodzie wynika, że chcąc poznać miarę kąta w przykładach z deltoidem, należy ustalić długości przyprostokątnych trójkąta prostokątnego i podstawić do wzorów w miejsce m i n podanych w poprzednim podrozdziale. W pierwszym pokazanym przykładzie, dla przypomnienia:

Rys. 3.21.
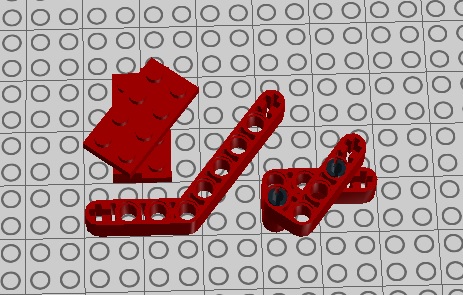
Rys. 3.22.

Rys. 3.23.
Kod: Zaznacz cały
długości boków obu trójkątów trójki Pitagorejskie
generujące taki sam ukos
1, 7, 5sqrt(2) 5, 5, 5sqrt(2) (3,4,5) (3,4,5)
1, 8, sqrt(65) 4, 7, sqrt(65) (5,12,13) (3,4,5)
2, 9, sqrt(85) 6, 7, sqrt(85) (8,15,17) (3,4,5)
2, 11, 5sqrt(5) 5, 10, 5sqrt(5) (7,24,25) (3,4,5)
3, 11, sqrt(130) 7, 9, sqrt(130) (5,12,13) (3,4,5)
1, 12, sqrt(145) 8, 9, sqrt(145) (3,4,5) (20,21,29)
1, 13, sqrt(170) 7, 11, sqrt(170) (8,15,17) (3,4,5)
4, 13, sqrt(185) 8, 11, sqrt(185) (12,35,37) (3,4,5)
3, 14, sqrt(205) 6, 13, sqrt(205) (9,40,41) (3,4,5)
5, 14, sqrt(221) 10, 11, sqrt(221) (5,12,13) (8,15,17)
9, 13, 5sqrt(10) 5, 15, 5sqrt(10) (7,24,25) (3,4,5)
3, 16, sqrt(265) 11, 12, sqrt(265) (28,45,53) (3,4,5)
1, 17, sqrt(290) 11, 13, sqrt(290) (3,4,5) (20,21,29)
4, 17, sqrt(305) 7, 16, sqrt(305) (11,60,61) (3,4,5)
1, 18, 5sqrt(13) 6, 17, 5sqrt(13) (7,24,25) (5,12,13)
1, 18, 5sqrt(13) 10, 15, 5sqrt(13) (33,56,65) (3,4,5)
6, 17, 5sqrt(13) 10, 15, 5sqrt(13) (16,63,65) (3,4,5)
7, 17, 13sqrt(2) 13, 13, 13sqrt(2) (5,12,13) (5,12,13)
2, 19, sqrt(365) 13, 14, sqrt(365) (3,4,5) (48,55,73)
3, 19, sqrt(370) 9, 17, sqrt(370) (12,35,37) (3,4,5)
4, 19, sqrt(377) 11, 16, sqrt(377) (5,12,13) (20,21,29)
7, 19, sqrt(410) 11, 17, sqrt(410) (9,40,41) (3,4,5)
8, 19, 5sqrt(17) 13, 16, 5sqrt(17) (7,24,25) (8,15,17)
5, 20, 5sqrt(17) 13, 16, 5sqrt(17) (36,77,85) (3,4,5)
5, 20, 5sqrt(17) 8, 19, 5sqrt(17) (13,84,85) (3,4,5)
1, 21, sqrt(442) 9, 19, sqrt(442) (5,12,13) (8,15,17)
2, 21, sqrt(445) 11, 18, sqrt(445) (39,80,89) (3,4,5)
9, 20, sqrt(481) 15, 16, sqrt(481) (12,35,37) (5,12,13)
1, 22, sqrt(485) 14, 17, sqrt(485) (3,4,5) (65,72,97)
3, 22, sqrt(493) 13, 18, sqrt(493) (8,15,17) (20,21,29)
8, 21, sqrt(505) 12, 19, sqrt(505) (20,99,101) (3,4,5)
1, 23, sqrt(530) 13, 19, sqrt(530) (28,45,53) (3,4,5)
2, 23, sqrt(533) 7, 22, sqrt(533) (9,40,41) (5,12,13)
4, 23, sqrt(545) 16, 17, sqrt(545) (60,91,106) (3,4,5)
6, 23, sqrt(565) 9, 22, sqrt(565) (15,112,113) (3,4,5)
7, 23, 17sqrt(2) 17, 17, 17sqrt(2) (8,15,17) (8,15,17)
9, 23, sqrt(610) 13, 21, sqrt(610) (11,60,61) (3,4,5)
2, 25, sqrt(629) 10, 23, sqrt(629) (12,35,37) (8,15,17)
11, 23, 5sqrt(26) 17, 19, 5sqrt(26) (7,24,25) (5,12,13)
5, 25, 5sqrt(26) 11, 23, 5sqrt(26) (16,63,65) (3,4,5)
5, 25, 5sqrt(26) 17, 19, 5sqrt(26) (33,56,65) (3,4,5)

Rys. 3.24.
4. Udawanie trójkąta prostokątnego.
Jeżeli przyprostokątne w trójkącie prostokątnym mają całkowitą długość, a przeciwprostokątna – niewiele większą od pewnej liczby całkowitej, można udawać, że trójkąt da się zbudować, minimalnie naprężając klocki. Jeżeli przyprostokątne mierzą 10 i 15, to przeciwprostokątna ma długość 5sqrt(13), czyli w przybliżeniu 18,028, co można zaokrąglić do 18. Edytor LDD nabiera się w tym przypadku i pozwala połączyć części:

Rys. 4.1.
Kod: Zaznacz cały
boki trójkąta prostokątnego przybliżona długość
przeciwprostokątnej
1 5 sqrt(26) 5,099
1 6 sqrt(37) 6,083
1 7 5sqrt(2) 7,071
5 5 5sqrt(2) 7,071
1 8 sqrt(65) 8,062
4 7 sqrt(65) 8,062
1 9 sqrt(82) 9,055
1 10 sqrt(101) 10,050
1 11 sqrt(122) 11,045
1 12 sqrt(145) 12,042
8 9 sqrt(145) 12,042
5 11 sqrt(146) 12,083
1 13 sqrt(170) 13,038
7 11 sqrt(170) 13,038
1 14 sqrt(197) 14,036
1 15 sqrt(226) 15,033
1 16 sqrt(257) 16,031
1 17 sqrt(290) 17,029
6 16 2sqrt(73) 17,088
1 18 5sqrt(13) 18,028
6 17 5sqrt(13) 18,028
10 15 5sqrt(13) 18,028
1 19 sqrt(362) 19,026
1 20 sqrt(401) 20,025
1 21 sqrt(442) 21,024
9 19 sqrt(442) 21,024
2 21 sqrt(445) 21,025
11 18 sqrt(445) 21,025
1 22 sqrt(485) 22,023
14 17 sqrt(485) 22,023
2 22 2sqrt(122) 22,091
1 23 sqrt(530) 23,022
13 19 sqrt(530) 23,022
2 23 sqrt(533) 23,087
7 22 sqrt(533) 23,087
Kod: Zaznacz cały
boki trójkąta prostokątnego przybliżenie długość
przeciwprostokątnej
4 8 4sqrt(5) 8,944
5 13 sqrt(194) 13,928
12 12 12sqrt(2) 16,971
6 18 6sqrt(10) 18,974
6 19 sqrt(397) 19,925
9 20 sqrt(481) 21,932
15 16 sqrt(481) 21,932

Rys. 4.2.
W zestawach firmowych sporą niespodzianką jest trójkąt tworzący tył kadłuba w 42025, Cargo Plane. Nigdy tych długości nie liczyłem, będąc przekonanym, że jest to któryś z większych trójkątów Pitagorejskich. Nic bardziej mylnego! Kąt prosty i wszystkie boki trójkąta są zrobione sztywno, ale ich długości to 9, 19 i 21 (licząc należycie, czyli między środkami otworów).
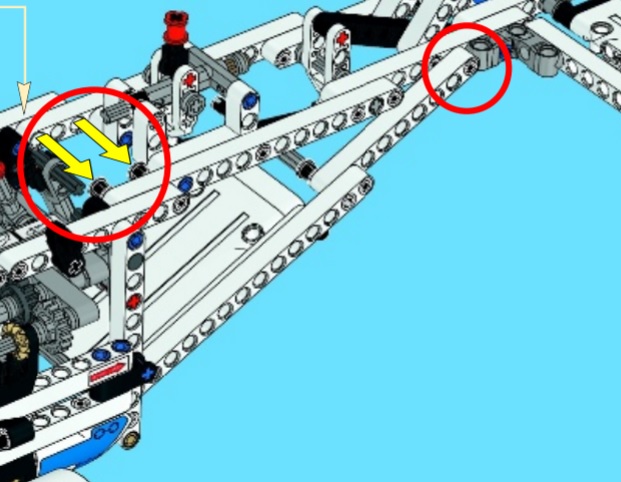
Rys. 4.3.
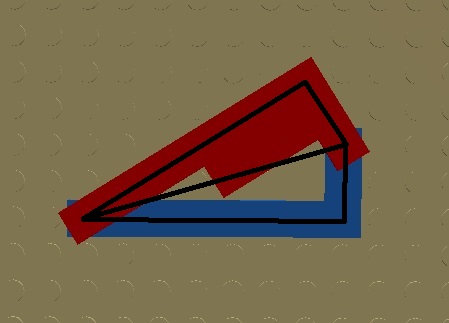
Drugim sposobem udawania, tym razem bez naprężeń, jest zbudowanie przeciwprostokątnej o całkowitej długości niepołączonej z wierzchołkami kątów ostrych, gdy prawdziwa przekątna powinna mieć długość nieznacznie dłuższą od budowanej. Na czerwono zbudowano trójkąt o bokach 5, 5, 5sqrt(2), imitując niewymierność liczbą 7, na niebiesko – trójkąt o bokach 1, 9, sqrt(82), zaokrąglając zapisany pierwiastek za pomocą liczby 9:

Rys. 4.4.
* klasycznie w 10182, Cafe Corner:

Rys. 4.5.

Rys. 4.6.
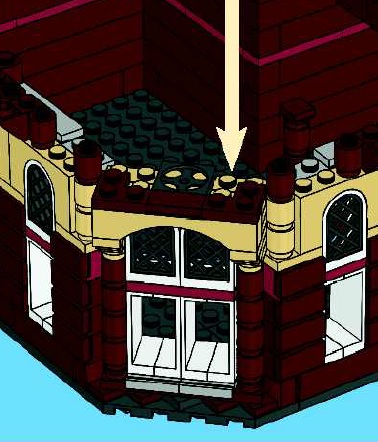
Rys. 4.7.

Rys. 4.8.

Rys. 4.9.
W lewym budynku 10255, Assembly Square, znajdziemy tego typu rozwiązanie, tylko z jeszcze większą szparą, bo wynikającą z trójkąta o bokach o długościach 3, 3, 3sqrt(2), czyli w przybliżeniu 4,243 zaokrąglane do 4:

Rys. 4.10.
Kod: Zaznacz cały
boki trójkąta prostokątnego przybliżona długość
przeciwprostokątnej
0,5 2 0,5sqrt(17) 2,062
0,5 3 0,5sqrt(37) 3,041
0,5 4 0,5sqrt(65) 4,031
2 3,5 0,5sqrt(65) 4,031
0,5 5 0,5sqrt(101) 5,025
0,5 6 0,5sqrt(145) 6,021
4 4,5 0,5sqrt(145) 6,021
2,5 5,5 0,5sqrt(145) 6,042
0,5 7 0,5sqrt(197) 7,018
0,5 8 0,5sqrt(257) 8,016
3 7,5 1,5sqrt(29) 8,078
0,5 9 2,5sqrt(13) 9,014
3 8,5 2,5sqrt(13) 9,014
5 7,5 2,5sqrt(13) 9,014
0,5 10 0,5sqrt(401) 10,012
4,5 9 4,5sqrt(5) 10,042
0,5 11 0,5sqrt(485) 11,011
7 8,5 0,5sqrt(485) 11,011
3,5 10,5 3,5sqrt(10) 11,068
0,5 12 0,5sqrt(577) 12,010
8,5 8,5 8,5sqrt(2) 12,021
3,5 11,5 8,5sqrt(2) 12,021
6 10,5 1,5sqrt(65) 12,093
1,5 12 1,5sqrt(65) 12,093
0,5 13 0,5sqrt(677) 13,010
1,5 13 0,5sqrt(685) 13,086
9 9,5 0,5sqrt(685) 13,086
0,5 14 0,5sqrt(785) 14,009
8 11,5 0,5sqrt(785) 14,009
1,5 14 0,5sqrt(793) 14,080
4 13,5 0,5sqrt(793) 14,080
6,5 12,5 0,5sqrt(746) 14,089
7,5 13 0,5sqrt(901) 15,008
0,5 15 0,5sqrt(901) 15,008
4 14,5 0,5sqrt(905) 15,042
5,5 14 0,5sqrt(905) 15,042
1,5 15 1,5sqrt(101) 15,075
0,5 16 2,5sqrt(41) 16,008
10 12,5 2,5sqrt(41) 16,008
4 15,5 2,5sqrt(41) 16,008
1,5 16 0,5sqrt(1009) 16,070
0,5 17 0,5sqrt(1157) 17,007
7 15,5 0,5sqrt(1157) 17,007
1,5 17 0,5sqrt(1165) 17,066
9 14,5 0,5sqrt(1165) 17,066
0,5 18 0,5sqrt(1297) 18,007
12,5 13 0,5sqrt(1301) 18,035
1,5 18 1,5sqrt(145) 18,062
12 13,5 1,5sqrt(145) 18,062
4,5 17,5 0,5sqrt(1306) 18,069
0,5 19 8,5sqrt(5) 19,007
8,5 17 8,5sqrt(5) 19,007
11 15,5 8,5sqrt(5) 19,007
4,5 18,5 5sqrt(58) 19,039
7,5 17,5 5sqrt(58) 19,039
9,5 16,5 5sqrt(58) 19,039
1,5 19 0,5sqrt(1453) 19,059
13,5 13,5 13,5sqrt(2) 19,092
Kod: Zaznacz cały
boki trójkąta prostokątnego przybliżona długość
przeciwprostokątnej
2,5 3 0,5sqrt(61) 3,905
2 4,5 0,5sqrt(97) 4,924
3,5 3,5 3,5sqrt(2) 4,950
3,5 6 0,5sqrt(193) 6,964
2,5 6,5 0,5sqrt(194) 6,964
2,5 7,5 2,5sqrt(10) 7,906
4,5 6,5 2,5sqrt(10) 7,906
5,5 7 0,5sqrt(317) 8,902
6,5 7 0,5sqrt(365) 9,925
3 9,5 0,5sqrt(397) 9,962
3 10,5 0,5sqrt(477) 10,920
4,5 10 0,5sqrt(481) 10,966
7,5 8 0,5sqrt(481) 10,966
5,5 9,5 0,5sqrt(482) 10,977
6,5 10 0,5sqrt(569) 11,927
7,5 10,5 1,5sqrt(74) 12,903
6 11,5 0,6sqrt(673) 12,971
3,5 12,5 0,5sqrt(674) 12,987
8,5 11 0,5sqrt(773) 13,901
3,5 13,5 0,5sqrt(778) 13,946
3,5 14,5 0,5sqrt(890) 14,916
9,5 11,5 0,5sqrt(890) 14,916
6,5 13,5 0,5sqrt(898) 14,983
11 11,5 0,5sqrt(1013) 15,914
10,5 12 1,5sqrt(113) 15,945
8,5 13,5 0,5sqr(1018) 15,953
5,5 15 0,5sqrt(1021) 15,977
5,5 16 0,5sqrt(1145) 16,919
9,5 14 0,5sqrt(1145) 16,919
4 16,5 0,5sqrt(1153) 16,978
11,5 12,5 0,5sqrt(1154) 16,985
10,5 14,5 0,5sqrt(1282) 17,903
7 16,5 0,5sqrt(1285) 17,923
9 15,5 0,5sqrt(1285) 17,923
4 17,5 0,5sqrt(1289) 17,951
11,5 15 0,5sqrt(1429) 18,901
4 18,5 0,5sqrt(1433) 18,927
4 19,5 0,5sqrt(1585) 19,906
8,5 18 0,5sqrt(1585) 19,906
9,5 18,5 0,5sqrt(1586) 19,912
12,5 15,5 0,5sqrt(1586) 19,912
7,5 18,5 0,5sqrt(1594) 19,962
10,5 17 0,5sqrt(1597) 19,981 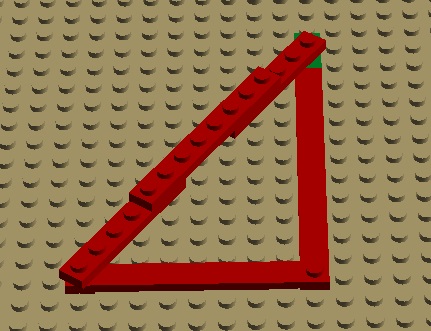
Rys. 4.11.

Rys. 4.12.

Rys. 4.13.

Rys. 4.14.
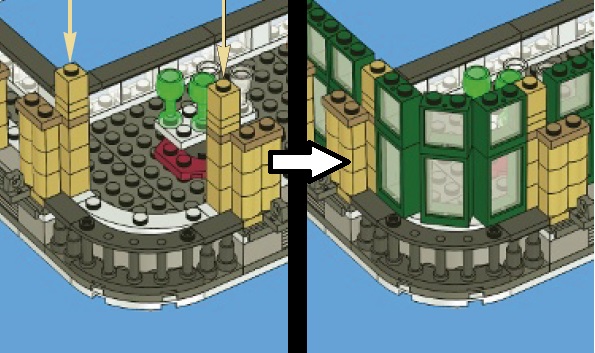
Rys. 4.15.
Budowanie z wariantem bez naprężenia pozostałych trójkątów stanowi trochę większy problem, ponieważ nie ma na środku studa położonego w równej odległości od końców przeciwprostokątnej, więc trzeba metodą prób i błędów szukać punktu zaczepienia lub zaczepiać na jednym z końców:

Rys. 4.16.

Rys. 4.17.

